2021-06-03 16:06:42 湘潭人事考试网 //hn.huatu.com/ 文章来源:湖南分院
巧解工程问题
工程问题是数量关系当中较为简单的题型,在往年的考试中经常出现,在数量关系部分占据了很重要的位置。其中核心的公式是工作总量=工作效率×工作时间。最基本的工程问题就是一条马路长2000米,每天翻修100米,问多少天能翻修完?
这里工作总量就是指这个工程总共需要完成多少,也就是这条马路的长2000米,而工作效率就是完成这项工程的快慢,也就是单位时间完成的量,在这里就是每天翻修100米,工作时间指的是完成这个项目所花费的时间。如果知道其中两个具体的量,势必可以求出另外一个未知量即
工作效率=工作量÷工作时间
工作时间=工作量÷工作效率
工作量=工作效率×工作时间。
平常考的多的往往是合作相关的问题,这个时候我们必须清楚多人的合作效率是相当于每个人的效率之和的。
工程问题主要分为三大类型:条件综合型、给定时间型、效率制约型。解决的方法通常是赋值法或者方程法。
小伙伴们可以先通过思维导图的形式了解一下解题的核心方法以及解题步骤:
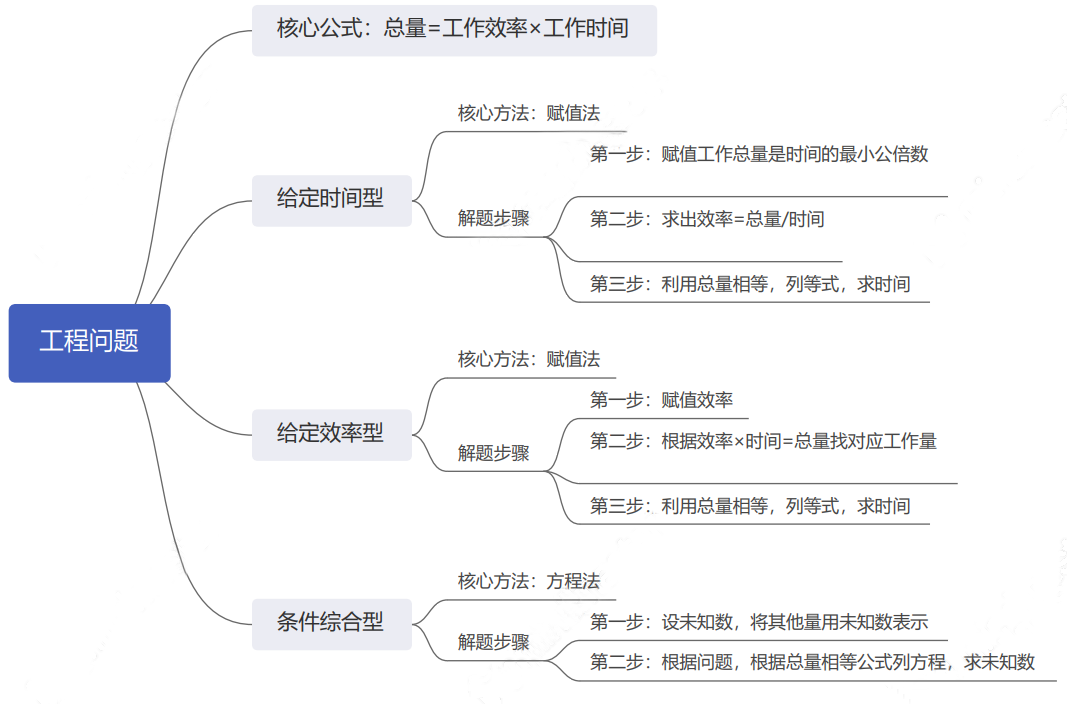
给定时间型
题目标志一般是题干给出不同的主语做工完成所需要的时间。
解题方法:
1.赋值工作总量(赋值给定时间的公倍数);
2.求出效率=总量/时间;
3.利用总量相等,列等式,求时间。
例如:某项工程,甲单独做需要20天,乙单独做需要30天,则甲乙合作完成这项工程需要多少天?
| 总量 | 工作效率 | 工作时间 | |
| 60 | 3 | 20 | 甲队 |
| 60 | 2 | 30 | 乙队 |
这里给出了不同主语做工完成所需要的时间,分别是甲20天、乙30天,所以可以赋值工作总量为60,那么甲的效率就是3,乙的效率就是2,甲乙进行合作的效率为5,所以根据工作时间=工作总量÷工作效率可得,甲乙合作需要12天。
效率制约型
题型标志一般是题干中直接或者通过计算得出不同主语的效率之比。
解题方法:
1.赋值工作效率;
2.求出总量=效率×时间;
3.利用总量相等,列等式,求时间。
例如:甲的效率与乙的效率之比为3:4,甲单独完成工作的时间是8天,则乙需要多少天完成这项工作?
| 总量 | 工作效率 | 工作时间 | |
| 24 | 3 | 8 | 甲队 |
| 24 | 4 | 6 | 乙队 |
这里直接给出了甲乙的效率之比,所以可以赋值工作效率甲为3,乙为4;根据甲的工作时间是8天,工作总量=工作时间×工作效率可得,这项工程得总量是3×8=24,故而乙的工作时间=24÷4=6天。
条件综合型
题型标志一般有效率、时间、总量三个量中的至少两个量的具体值。我们一般采取方程法来解决此类问题。
例如:某装配式建筑企业接到一个生产1033套楼板的订单。甲班组生产5天后,乙班组再生产4天,刚好完成任务。若甲班组比乙班组每天多生产23套,则甲班组生产楼板的套数是
A.625套
B.645套
C.535套
D.515套
根据题意可知,此题不仅给定了工作总量,还给定了工作时间,所以此题属于条件综合型。根据核心公式工作总量=工作时间×工作效率,运用方程法解题。设乙每天的工作效率为X,那么甲每天的工作效率为X+23。可列方程:5(x+23)+4x=1033,解得x=102,那么甲班组每天生产102+23=125(套),则甲班组生产楼板的套数为125×5=625(套)。
(编辑:hnhuatu01)上一篇:2022湘潭国家公务员考试行测备考:浅谈资料分析与数量关系
下一篇:没有了


20000
每日阅读20000+
粉丝20000+
每日转发

华图官方微信
微信号:18173153264
报名地址:长沙市芙蓉区五一大道新华大厦四楼华图教育
报名网址:
changsha.huatu.com/